吉野貴晶のクオンツトピックス

No.27
ブラックリッターマンモデルとベイズ統計

2024年11月15日号

写真（吉野）

投資工学開発部
吉野 貴晶

金融情報誌「日経ヴェリタス」アナリストランキングのクオンツ部門で16年連続で1位を獲得。ビックデータやAI（人工知能）を使った運用モデルの開発から、身の回りの意外なデータを使った経済や株価予測まで、幅広く計量手法を駆使した分析や予測を行う。

写真（木村）

投資工学開発部
木村 嘉明

ニッセイアセット入社後、リスク管理、国内外株式領域のリサーチ・運用業務等に従事。2022年4月より投資工学開発部において、主に計量的手法・AIを活用したクオンツリサーチおよび投資戦略の開発を担当。

写真（塚本）

投資工学開発部
塚本　恵

ニッセイアセット入社後、投資工学開発部にて主に機械学習を含む数理的な定量的手法、オルタナティブデータを活用した新たな投資戦略の研究開発を担当。

期待リターンの確率分布をベイズ統計の視点で考察してみよう

  • 期待リターンの推定誤差と最適化問題の解の変動について
  • ベイズ更新による期待リターン分布のブレンドとブラックリッターマンモデルについて

0. 予備知識、キーワード

基本的な金融工学、統計学の知識を仮定します。

キーワード
平均分散法、ブラックリッターマンモデル、確率分布、ベイズ統計、シミュレーション

1. イントロダクション

ロボアドバイザーのポートフォリオ構築（資産配分）でよく使われているブラックリッターマンモデルですが、ベイズ統計学的な視点で考察することも可能です。前回記事のNo.26（以下、前回と省略）では、平均分散法またはブラックリッターマンモデルを用いて、ポートフォリオ最適化の解を導出し、その特徴について考察しました。今回は、より統計学的な視点で考察をしていきます。

期待リターンの推定と平均分散法、ブラックリッターマンモデル

2. 期待リターンの分布

前回同様、国内外の株式債券の4資産をメインの計算の対象とします。各資産のリターンの分布を考える上で、想定より下振れ確率が大きい論点（いわゆるテールリスク）もありますが、ここでは各資産のリターンの分布が正規分布に従うことを仮定します。期待リターンの推定では必ずブレが生じ、言い換えると確率的なものと考えることができます。以下の（図1）は、国内株式の期待リターンの確率分布（他の資産も同様）であり、（図2）は、期待リターンの推定値をブレさせて平均分散法による最適化を10回行なった場合の解のばらつき具合です。

図1：国内株式の期待リターン分布（他の資産も同様のため割愛）

図2：平均分散法の反復試行による解の変動

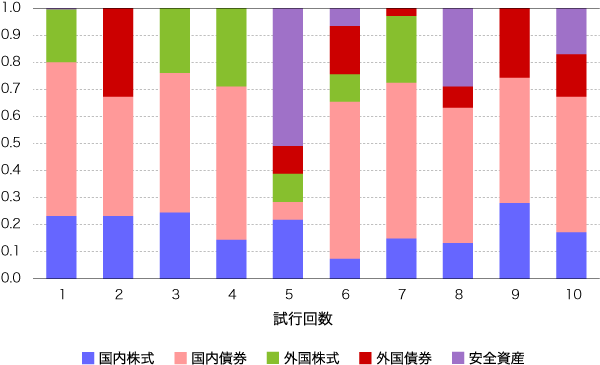
前回も述べましたが、期待リターンの推定値が少し変わるだけで、最適化の結果が大きく変わる点が上記で確認できました。一方、市場ポートフォリオから逆算された均衡期待リターンとの混合推定を用いた平均分散法（ブラックリッターマンモデル）では、最適化が極端な結果になりにくいという特徴があります。以下の（表1）は今回使用する均衡期待リターンと投資家独自の見通しとなります。（図3）は、これらを用いてブラックリッターマンモデルによる最適化を10回行なった場合の結果で、解の挙動が安定しています。

表1：均衡期待リターンと投資家独自の見通し

  国内株式(％) 国内債券(％) 外国株式(％) 外国債券(％) 安全資産(％)
均衡期待リターン 8.4 1.8 7.9 3.7 1.0
投資家独自の見通し -4.0 2.0 8.0 5.0 1.0

図3：ブラックリッターマンモデルを用いた反復試行による解の変動

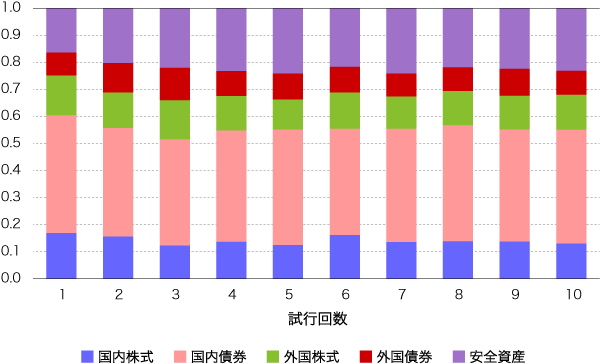
次節以降では、このことについてベイズ統計の立場から考察を進めていきます。

ベイズの定理による確率の更新

3. ベイズ統計のおさらい

本節では、ベイズ統計についての基本的な考え方をおさらいしていきます。
ベイス統計とは、従来の頻度主義とは異なる統計学の理論であり、観測データと事前情報を組み合わせ、確率を更新する手法です。ベイズの定理に基づき、観測データが与えられた後の「事後確率」を求めます。これにより、逐次的な情報更新が可能になります。パラメータ自体にも確率を割り当てるため、複雑なモデルに対応しやすい利点があり、現在も機械学習などの多様な分野で利用されています。

まず、考え方の中核であるベイズの定理について説明します。定理のステートメントは以下の数式であり、条件付き確率に関する対称性を主張しています。ここで、\(P(A\hspace{0.1em}|B)\)は事象\(B\)が起こるという条件下で事象\(A\)が起こる条件付き確率、別の言い方では\(B\)が与えられたときの\(A\)の事後確率といいます。

\( P(A\hspace{0.1em}|B)=P(B\hspace{0.1em}|A) \dfrac{P(A)}{P(B)} \) 　（1）

例を考えてみましょう。赤い箱、青い箱それぞれにりんご2個オレンジ6個、りんご3個オレンジ1個入っているとし、箱をランダムに選んで中の果実を1つ取り出す試行を行うとします。このとき、40％の確率で赤い箱が選ばれるとします。ベイズの定理を用いると、オレンジを選んだときに、それがどの箱から選んだものかに関する確率が計算できます。箱を選ぶ事象を\(𝐴=\{𝑟, 𝑏\} \)とし、果実を選ぶ事象を\(𝐵=\{𝑎, 𝑜\} \)とします。ベイズの定理から、オレンジを選んだときに、それが赤箱から選ばれた確率は

\( P(A=r\hspace{0.1em}|B=o)=P(B=o\hspace{0.1em}|A=r)\dfrac{P(A=r)}{P(B=o)}=\dfrac{3}{4}\times\dfrac{4}{10}\div\dfrac{9}{20}=\dfrac{2}{3} \)

となります。ただし、\(P(A)\) は事前確率とも呼ばれ、非自明な \(P(B)\)は以下のように計算できます。

$$ P(B=a)=P(B=a\hspace{0.1em}|A=r)P(A=r)+P(B=a\hspace{0.1em}|A=b)P(A=b) $$ $$ =\dfrac{1}{4}\times\dfrac{4}{10}+\dfrac{3}{4}\times\dfrac{6}{10}=\dfrac{11}{20} $$ ⇒ \( P(B=o)=1-P(B=a)=1-\dfrac{11}{20}=\dfrac{9}{20} \)

元々、赤い箱が選ばれる確率\(P(A=r)\)（事前確率）は40%だったので、「オレンジを選んだ」という観測データから、事後確率は\(P(A=r|B=o) =2/3≒67\%\)と赤い箱の確率が高まります。赤い箱の方がオレンジの比率が高いので、これは直観的にも理解できます。ベイズの定理から得られるこの構造をベイズ更新と呼び、ブラックリッターマンモデルにおいても、このベイズ更新の枠組みを当てはめることが可能です。
また、一般に事象\(A、B\)は、必ず起こるという決定論的な仮定を置いている場合が多いですが、実際は確率的な事象も存在します。（1）のベイズの定理も拡張して考えることが可能で、事象\(P、Z\)が確率変数である場合（2）が成り立ちます。(\(p\hspace{0.1em}df\)は確率密度関数、\(\propto\)は比例記号)

\( p\hspace{0.1em}df(p\hspace{0.1em}|z)=p\hspace{0.1em}df(z\hspace{0.1em}|p)\dfrac{p\hspace{0.1em}df(p)}{p\hspace{0.1em}df(z)}\propto p\hspace{0.1em}df(z\hspace{0.1em}|p)p\hspace{0.1em}df(p) \) 　(2)

（2）は事前分布（事前確率）に尤度（観測データ）を掛け合わせることにより、更新された事後分布（事後確率）を得るということを意味しています。

ベイズ更新と混合リターン分布

4. ブラックリッターマンモデルとベイズ統計

ブラックリッターマンモデルは、均衡期待リターンと投資家独自の見通しを混ぜ込んで新たなリターン（混合リターン）を形成しており、これをベイズ統計の視点でみると、次の対応関係で考えることができます。

表2：ベイズ統計の視点でみたブラックリッターマンモデル

事前分布 観測データ 事後分布
投資家独自の見通しの分布 均衡期待リターンの分布 混合リターンの分布

本節では、可視化のため国内株式と外国債券の2資産に限定して、各リターン分布のグラフを描写します。（数学的には2資産方向への射影を考えるだけで、高次元化しても本質は同じです。）

図4：投資家独自の見通しと均衡期待リターン、混合リターン分布の確率密度関数の等高線

※\(\tau\)は0.2とする

（図4）は、国内株式が-4%、外国債券が5%という投資家独自の見通しを、均衡期待リターンと混ぜこむことで、これらの見通しを反映した混合リターンが得られるということを意味しています。前回、均衡期待リターンの信頼度を表すパラメータ\(\tau\)を紹介しましたが、これは\(\tau\)が小さい（大きい）ほど均衡期待リターンへの信頼が大きい（小さい）というものでした。
混合推定とベイズの定理に関する数学的な定式化は次節で行いますが、本節では最後に、\(\tau\)を変化させた場合の混合リターン分布の推移を確認します。1段目左が最も\(\tau\)が小さく、そこから右→下段にいくにつれて投資家独自の見通しに近づいていくことが確認できます（図5）。

図5：\(τ\)を変化させた場合の混合リターン分布の推移

5. 数学的定式化

前回同様、均衡期待リターンと投資家独自の見通しが以下の分布に従うと仮定します。

\( \Pi = \mu + \delta,　\delta ～ N(0, \tau\Sigma) \)　（3）
\( Q = P\mu + \varepsilon,　\varepsilon ～ N(0, \Omega) \)　（4）

ベイズの定理と、多変量正規分布の確率密度関数の形からある定数\(k\)が存在して

$$ p\hspace{0.1em}df(\mu^* | \pi) = p\hspace{0.1em}df(\pi|\mu^*)\dfrac{p\hspace{0.1em}df(\mu^*)}{p\hspace{0.1em}df(\pi)} \left( = p\hspace{0.1em}df(\pi|\mu^*)\dfrac{p\hspace{0.1em}df(P\mu^*)}{p\hspace{0.1em}df(\pi)} \right)\\[3em] = \dfrac{k\cdot exp\left\{ - \dfrac{1}{2}(\pi - \mu^*)^T(\tau\Sigma)^{-1}(\pi - \mu^*) - \dfrac{1}{2}(P\mu^* - q)^T\Omega^{-1}(P\mu^* - q) \right\}}{p\hspace{0.1em}df(\pi)}\\[3em] \propto exp \left\{ - \dfrac{1}{2}(\mu^* - H^{-1}C)^TH(\mu^* - H^{-1}C) \right\} $$

を得ます。ただし

\( H = P^T\Omega^{-1}P + (\tau\Sigma)^{-1},　C = P^T\Omega^{-1}q + (\tau\Sigma)^{-1}\pi \)

以上から、この事後分布における期待値は以下の通りになります。

\( E\hspace{0.1em}[\mu\hspace{0.1em}|\Pi] = H^{-1}C = \{P^T\Omega^{-1}P + (\tau\Sigma)^{-1}\}^{-1}\{ P^T\Omega^{-1}Q + (\tau\Sigma)^{-1}\Pi \} \)　（5）

（5）の結果は、前回の一般化最小二乗法（GLS）で求めた期待リターンの推定値と一致しており、ベイズ統計的な手法でも、ブラックリッターマンモデルにおける混合推定リターンが導出されることが確認できました。

まとめ

6. まとめ

ベイズ統計を通して考えると、ブラックリッターマンモデルには、投資家が市場データと自身の見解をバランス良く反映した戦略を立て、新たな情報にも迅速に対応できるという長所があることが分かります。
ベイズ統計を金融工学に応用したように、今後も異分野の知見を融合させることで、投資戦略の新たなアイデアが生まれていくことが期待できます。

参考文献

  • [TH・KT] 津田博史,小松高広,最適投資戦略,朝倉書店,（2018）
  • [Bishop] C.M.ビショップ,他訳,パターン認識と機械学習上ベイズ理論による統計的予測,丸善出版,（2012）
  • [SS] Satchell, Scowcroft, A demystification of the Black–Litterman model: Managing quantitative and traditional portfolio construction,（2000）

吉野貴晶のクオンツトピックス一覧へ

「吉野貴晶のクオンツトピックス」ご利用にあたっての留意点

当資料は、市場環境に関する情報の提供を目的として、ニッセイアセットマネジメントが作成したものであり、特定の有価証券等の勧誘を目的とするものではありません。

【当資料に関する留意点】

  • 当資料は、信頼できると考えられる情報に基づいて作成しておりますが、情報の正確性、完全性を保証するものではありません。
  • 当資料のグラフ・数値等はあくまでも過去の実績であり、将来の投資収益を示唆あるいは保証するものではありません。また税金・手数料等を考慮しておりませんので、実質的な投資成果を示すものではありません。
  • 当資料のいかなる内容も、将来の市場環境の変動等を保証するものではありません。
  • 手数料や報酬等の種類ごとの金額及びその合計額については、具体的な商品を勧誘するものではないので、表示することができません。
  • 投資する有価証券の価格の変動等により損失を生じるおそれがあります。